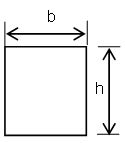
Area: \( A = b \times h \)

Centroid: \( \bar{x} = \frac{b}{2} \)

Centroid: \( \bar{y} = \frac{h}{2} \)

Area: \( A = \pi R^2 \)

Centroid: At center

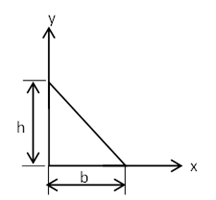
Area: \( A = \frac{1}{2} b h \)

Centroid: \( \bar{x} = \frac{b}{3} \)

Centroid: \( \bar{y} = \frac{h}{3} \)

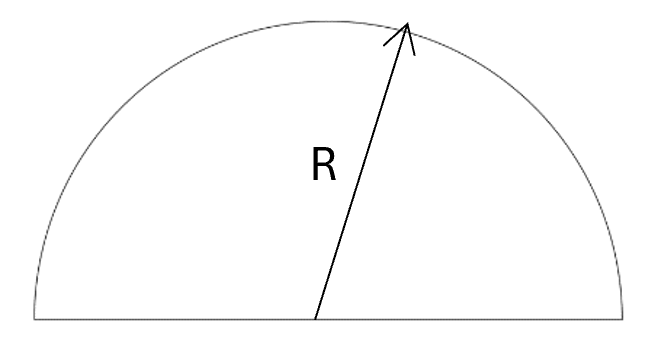
Area: \( A = \frac{1}{2}\pi R^2 \)

Centroid: \( \bar{x} = 0 \)

Centroid: \( \bar{y} = \frac{4R}{3\pi} \)

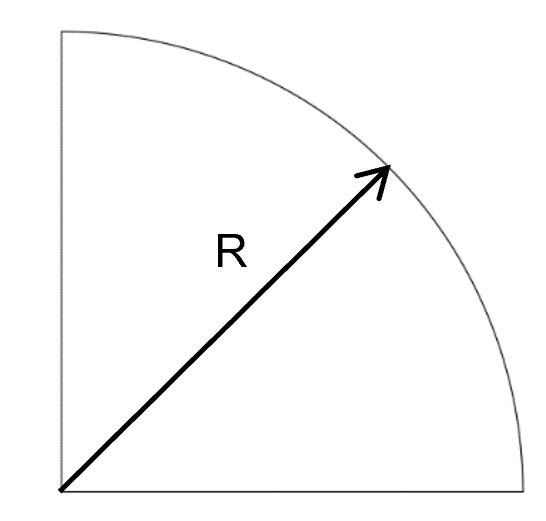
Area: \( A = \frac{1}{4} \pi R^2 \)

Centroid: \( \bar{x} = \frac{4R}{3\pi} \)

Centroid: \( \bar{y} = \frac{4R}{3\pi} \)

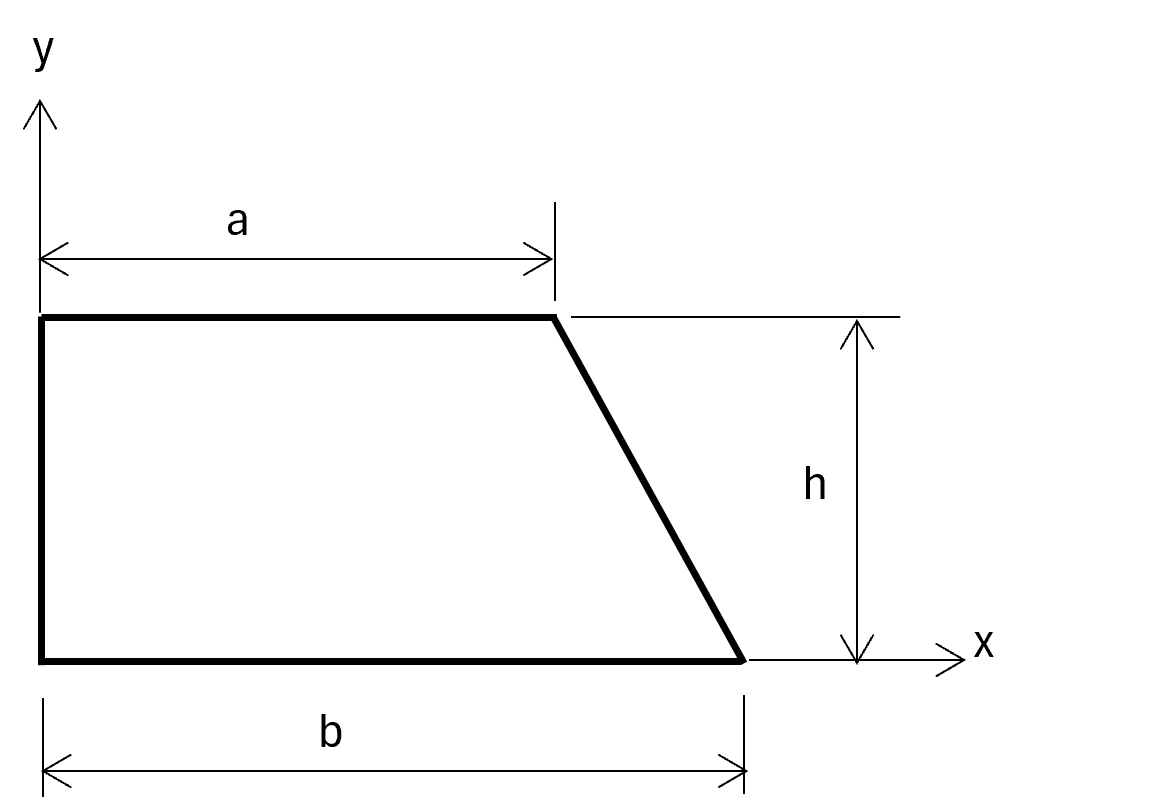
Area: \( A = \frac{1}{2} (a + b) h\)

Centroid: \( \bar{x} = \frac{a^2 + b^2+ab}{3(a+b)} \)

Centroid: \( \bar{y} = \frac{h(2a+b)}{3(a+b)} \)

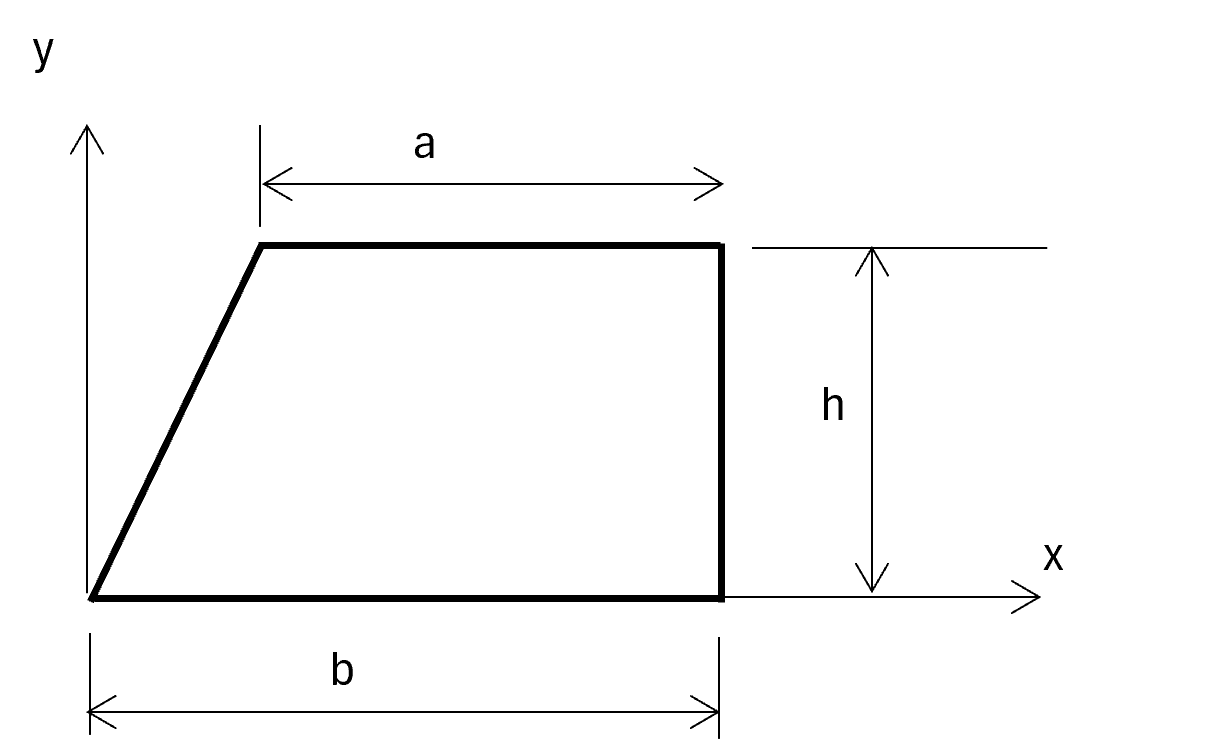
Area: \( A = \frac{1}{2} (a + b) h\)

Centroid: \( \bar{x} = \frac{b^2 -2 a^2+ab}{3(a+b)} \)

Centroid: \( \bar{y} = \frac{h(2a+b)}{3(a+b)} \)

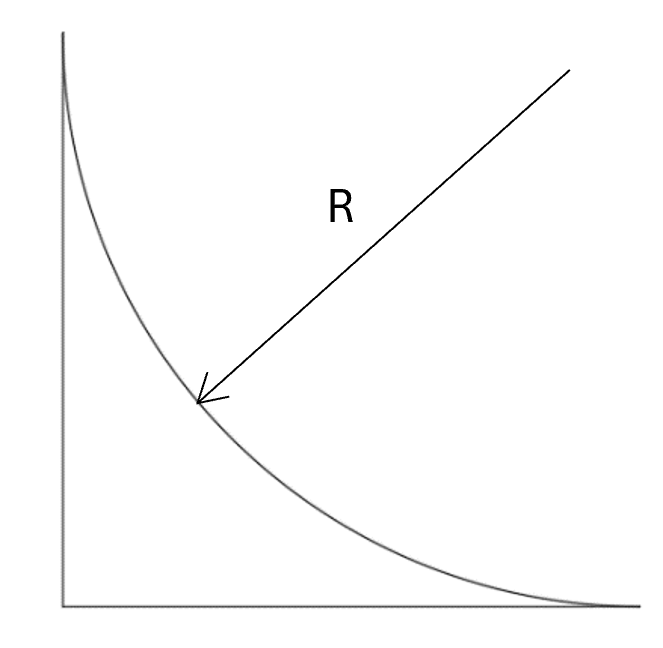
Area: \( A = R^2 (1 - \frac{\pi}{4}) \)

Centroid: \( \bar{x} = R\frac{(10-3\pi)}{12(1-\frac{\pi}{4})} \)

Centroid: \( \bar{y} = R\frac{(10-3\pi)}{12(1-\frac{\pi}{4})} \)

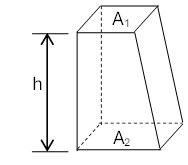
Volume: \( V = \frac{h}{3} (A_1+A_2+\sqrt(A_1A_2)) \)

Centroid: \( \bar{y} = \frac{h}{4}\frac{(A_1+3A_2+2\sqrt(A_1A_2))}{(A_1+A_2+\sqrt(A_1A_2))} \)