DESIGN OF CONCRETE SECTION AS PER BS 8110: 1997
MATERIAL SAFETY FACTORS
The material safety factors have been assumed for concrete and steel as given below
For Concrete \( \gamma_m = 1.5 \)
For Steel \( \gamma_m = 1.15 \)
Shear strength without reinforcement \( \gamma_m = 1.25 \)
Bond Strength \( \gamma_m = 1.40 \)
Others \( \gamma_m = 1.50 \)
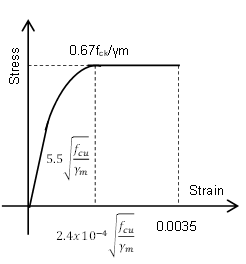
STRESS-STRAIN CURVE OF CONCRETE
The stress-strain relationship of concrete shall be parabolic and can be represented by following curve.
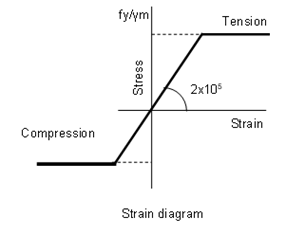
STRESS-STRAIN CURVE OF STEEL
Stress-strain curve is linear as given below. The relation is shown as given below.
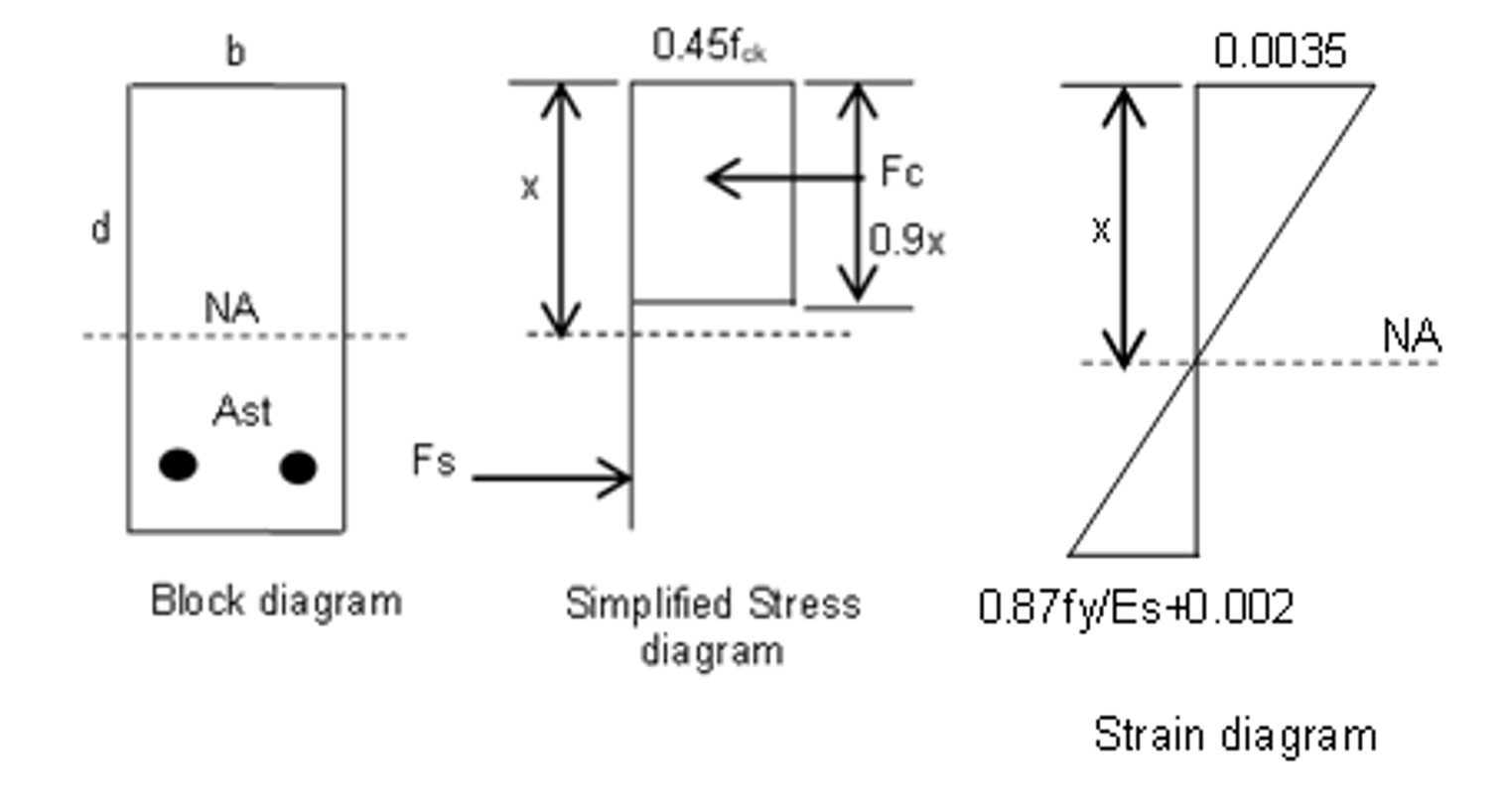
STRESS AND STRAIN DIAGRAM OF THE SECTION
The relation is given as follows.
Constant \( K'=0.156 \) where redistribution does not exceed 10% (this implies a limitation of the neutral axis depth to \(\frac{d}{2}\)); Otherwise \(K'=0.402(\beta-0.4)-0.18(\beta-0.4)^2 \) where redistribution exceeds 10%
If \(K>K'\), the section is doubly reinforced, otherwise singly reinforced. Where the ratio
1. Design of singly reinforced section
If \(K'>K\), the section is singly reinforced section and designed as follows
Calulation of moment arm, \(z\)
but \(Z\) should not be greater than \(0.95d\)
Depth of neutral axis
Area of reinforcement is now given by
2. Design of Doubly reinforced section
If \(K>K'\), the section is doubly reinforced section and designed as follows
Calulation of moment arm, \(z\)
but \(Z\) should not be greater than \(0.776887d\)
Depth of neutral axis
Now, area of reinforcement is given by,
Total area of tension reinforcement is given by;
Compression reinforcement is given by
If \(\frac{d’}{x} \) exceeds 0.37 (for \(f_y=500N/mm^2\)), the compression stress will be less than \(f_{sc} = 0.87f_y\) and obtained from stress-strain curve of reinforcement
SHEAR REINFORCEMENT
Design shear stress of section is given by.
In no case, \( v \leq v_{max} \) where \(v_{max}= min. of (0.8\sqrt{f_{cu}}, 5 N/mm^2 \) )
Shear strength shall be calculated by;
Where,
Which should not be less than 1.
For Plain concrete and \( k_2 > 1 \) for reinforced concrete.
and
\( k_3 \geq 1\)\( f_{cu}\) should not be greater than 40 N/mm2
\( v_c\) is given in Table 3.8 of BS8110.1.
Form and area of shear reinforcement in beam
1. If \(v<0.5v_c \), No shear reinforcement required.
2. If \( v_c+0.4 \leq v \leq 0.8 \sqrt(f_{cu}) or 5N/mm^2 \), then Minimum links for whole length shall be provided.
3. \(v>(v_c+0.4)\) and \(v\leq 0.8\sqrt(f_{cu})\) or 5 N/mm2.
In case of shear reinforcement in slab \(0.5v_c\) shall be replaced by \(v_c\). Generally, it is not recommended to provide shear reinforcement. Thickness shall be increased if \(v>v_c\).
MINIMUM AND MAXIMUM REINFORCEMENT
As per Table 3.25- Minimum percentage of reinforcement as follows;
Section subjected to pure tension
1. Tension reinforcement
2. Compression reinforcement (Rectangular column)
3. Rectangular beam
In case of Fe415, interpolation shall be carried out.
In slab, minimum reinforcement = \(0.13\)%
Maximum reinforcement = \(4\)% in flexure and 6% in vertically cast columns
The design of One-way slab is similar to Beam design.