PREPARATION OF INTERACTION DIAGRAM AS PER IS456:2000
To prepare the interaction diagram, four different cases shall be fulfilled.
a) When the neutral axis is at infinity, i.e. \(kD\to \infty \), pure axial load is applied on the column.
b) When the neutral axis is outside the cross-section of the column i.e. \(∞>kD \geq D\).
c) When the neutral axis is within the cross-section of the column i.e \( kD \leq D\).
d) When the column behaves like a steel beam.
a) WHEN THE NEUTRAL AXIS IS AT INFINITY \(kD\to \infty \), PURE AXIAL LOAD IS APPLIED ON THE COLUMN
The strain profile EF represents the condition of pure compression. The pure axial force of concrete and steel are given as.
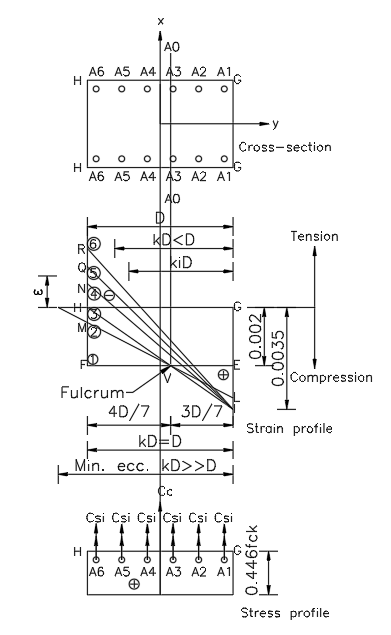
Pure compresive force of concrete
Pure compresive force of Steel
Total compressive force at the section
Now
And
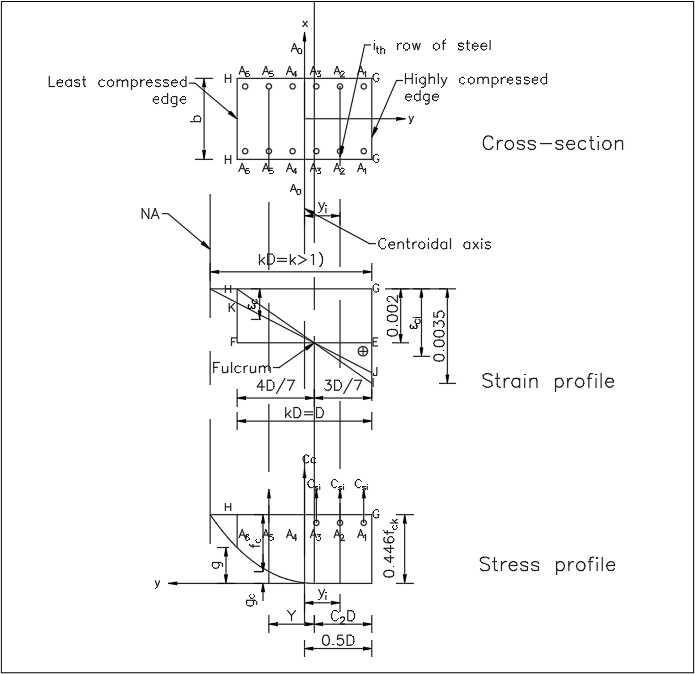
b) WNEN THE NEUTRAL AXIS IS OUTSIDE THE CROSS-SECTION OF THE COLUMN i.e. \(∞>kD \geq D\).
The strain profile JK in above diagram represents this condition
And Moment is given by;
Where,
So,
The values of \(C_1\) and \(C_2\) are given in the Table below.
Here,
| \(K\) | \(C_1\) | \(C_2\) |
|---|---|---|
| 1.00 | 0.361 | 0.416 |
| 1.05 | 0.374 | 0.432 |
| 1.10 | 0.384 | 0.443 |
| 1.20 | 0.399 | 0.458 |
| 1.30 | 0.409 | 0.468 |
| 1.40 | 0.417 | 0.475 |
| 1.50 | 0.422 | 0.480 |
| 2.00 | 0.435 | 0.491 |
| 2.50 | 0.440 | 0.495 |
| 3.00 | 0.442 | 0.497 |
| 4.00 | 0.444 | 0.499 |
Computation of compressive stress of Concrete
If Strain \(ε<0.002\) the stress \(f_c\) is given by:
Otherwise if
stress is given by,
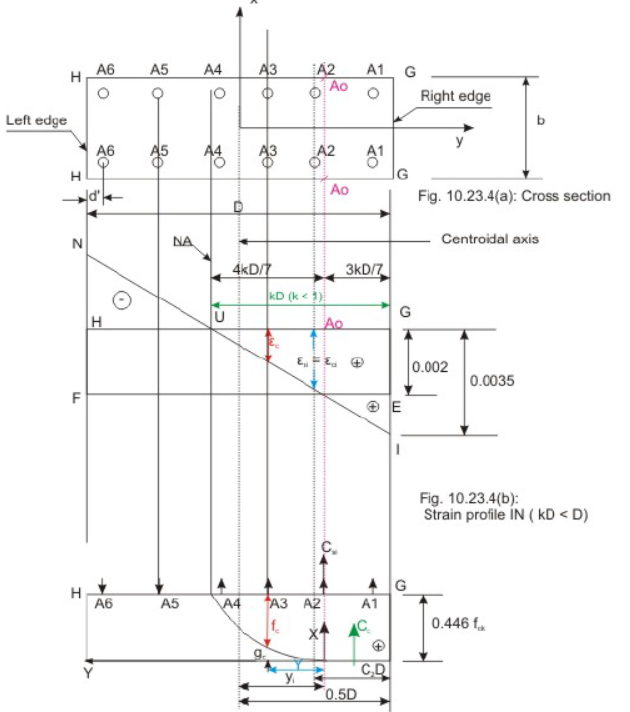
c) WHEN THE NEUTRAL AXIS IS WITHIN THE CROSS-SECTION OF THE COLUMN i.e \( kD \leq D\).
Compressive force of Concrete
Compressive force of Steel
Total compressive force
And Moment Capacity is given by;
And
d) WHEN THE COLUMN BEHAVES LIKE A STEEL BEAM
This condition occurs when the column is subjected to pure moment only i.e., \(M_u=M_o\)
So,
And Moment Capacity is given by;
And
By fulfilling these conditions, the interaction diagram can be prepared.